К методике обратного вычисления темпа роста рыб с использованием регрессионной зависимости между размерами тела и чешуи

Идея написания этой статьи возникла в результате долгих безуспешных поисков методик обратного вычисления темпа роста рыб с использованием уравнений регрессии. Упоминание этих методов встречаются в зарубежных статьях и рефератах (Francis, 1990; Escot, Granado-Lorencio, 1999), однако сами процедуры вычисления и формулы найти не удалось. Поэтому я попытался вывести такие формулы. Буду благодарен за критические замечания и сообщения о вероятных (весьма вероятных) ошибках.

В основе метода обратных вычислений темпа роста лежит утверждение о наличии определенной зависимости между размерами тела и регистрирующей структуры (обычно это чешуя). Простейший способ определения темпа роста, предложенный Э. Леа (Брюзгин,1969) предполагает прямую пропорциональную зависимость:

l_c/l_i = S_c/S_i, где l_c и S_c - соответственно, размеры тела и чешуи в момент поимки, а l_i и S_i - то же на i-том году жизни.

Хотя многими исследователями доказана неточность данного метода (Брюзгин, 1969; Мина, Клевезаль, 1976), он получил широкое распространение благодаря своей простоте. В данной формуле не учитывается размер малька на момент формирования чешуйного покрова. Поэтому, при линейной зависимости вида l = a+bS, когда линия регрессии не проходит через начало координат предпочтительнее формула Р. Ли (Брюзгин, 1969):

l_i=l_c(S_i/S_c)+a(1-S_i/S_c).

Однако, функция, описывающая связь размеров тела и регистрирующей структуры не всегда бывает линейной (Брюзгин,1969).

Вероятно, при нелинейной зависимости используется отношение:

l_c/l_i = f(S_c)/f(S_i), где, как и в формуле Р.Ли, f(x) - уравнение регрессии, описывающее зависимость l(S).

Так были получены следующие формулы:

1. Степенная регрессия: l(S)=aS^b
=>

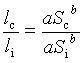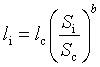
2. Показательная регрессия: l(S)=ab^S
=>

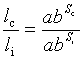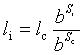
3. Экспоненциальная регрессия: l(S)=ae^bS
=>

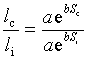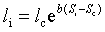
4. Параболическая регрессия: l(S)=a+bS+cS²
=>

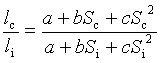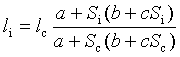
Я пользовался формулами, полученными из уравнений регрессии l(S). Биологического смысла такая зависимость не имеет, однако исследователи используют ее чаще, чем S(l) (формула Р. Ли также основана на зависимости "длина-чешуя"), да и формулы выходят менее громоздкими.

Одна из формул (для степенной регрессии) опробована при определении темпа роста обыкновенной востробрюшки из пяти водоемов среднего течения реки Сырдарья. В четырех выборках из пяти зависимость l(S) описывалась степенной регрессией и только в одной - линейной. Во всех четырех случаях, при использовании метода Э. Леа наблюдался "феномен Ли". В данных же, полученных по приведенной выше формуле (1), он отсутствовал.

Литература

1. Брюзгин В.Л. Методы изучения роста рыб по чешуе, костям и отолитам. - Киев: Наукова думка, 1969.
2. Мина М.Ф., Клевезаль Г.А. Рост животных. - М.: Наука, 1976.
3. Escot C., Granado-Lorencio C. Comparison of four methods of back-calculating growth using otoliths of a European barbel, Barbus sclateri (Gunther) (Pisces : Cyprinidae) // Mar. Freshwater Res. 1999, 50, 83.
4. Francis R. I. C. C. Back-calculation of fish length: a critical review // J. Fish Biol. 1990, 36. No 6. P. 883-902.