On the regression methods of back-calculation of the fish growth

I decided to write this article after long unsuccessful searches in literature of regression methods of growth back-calculation.

The problem is literature shortage in our country. I saw a mention of these methods in some abstracts (Francis, 1990; Escot, Granado-Lorencio, 1999). However, I couldn't find the formulas and procedures of calculation. Therefore, I have tried to derive those formulas.

I will highly appreciate censorious remarks and messages about probable (highly probable) errors as well as receiving the correct formulas.

The growth of a fish is periodic. Therefore, the hard parts of a fish (scales, otoliths, bones or fin rays) have annual marks like those in a tree. Age estimating and growth history study methods use those natural data loggers. The basic assumption for back-calculation methods is that there is a certain relationship between body length and scale (here and below for the sake of simplicity "scale" but it may be otoliths, bones, etc.) size. The elementary way of back-calculating growth offered by E. Lea assumes direct proportionality relationship:

l_c/l_i = S_c/S_i, (1)

Where l_c is the length at capture, l_i is the back-calculated length at age i, S_c is the scale size at capture, S_i is the measured size of the scale at age i.

But this equation does not consider fry size at the scale forming moment. So in case line l(S) does not pass through point (0, 0) more preferable is Fraser-Lee equation based on the straight-line regression l= a+bS:

l_i=l_c(S_i/S_c)+a(1-S_i/S_c). (2)

But very often length-scale regression is non-linear. I surmise that in this case is used the same proportion as in (1, 2):

l_c/l_i = f(S_c)/f(S_i), (3)

Where f(x) is the length-scale regression.

So based on this [presumption] I tried to derive following back-calculating formulas:

1. Power l(S)= aS ^b
=>

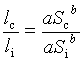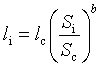
2. Compound l(S)= ab^S
=>

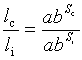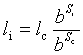
3. Exponential l(S)= ae^bS
=>

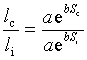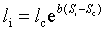
4. Quadratic l(S)= a + bS + cS ²
=>

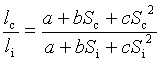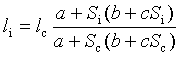
One of those formulas (for the power regression) was tested on five samples of common sawbelly Hemiculter leucisculus (Basilewsky) from different waterbodies of the Syr-Darya River. The length-scale relationship of four of five samples is described by power regression and only for the one by linear. In data obtained by using Lea's method for all that four samples Lee's phenomenon is manifested. But it is not observed when regression method is used.

References

1. Escot C., Granado-Lorencio C. Comparison of four methods of back-calculating growth using otoliths of a European barbel, Barbus sclateri (Gunther) (Pisces : Cyprinidae) // Mar. Freshwater Res. 1999, 50, 83.
2. Francis R. I. C. C. Back-calculation of fish length: a critical review // J. Fish Biol. 1990, 36. No 6. P. 883-902.